[Course 2 of the GPU programming specialization on coursera by John Hopkins University]
Introduction to CUDA Programming -
Objectives:
- dissect complex linear and multidim problems into kernels that execute on 100s to 1000s of threads
- transfer data between CPU host and GPU device memoryy
- utilize shared & constant memory on the GPU to communicate static & dynamic data between threads & blocks
- place small subsets of data into register memory allocated to threads for better performance and data coherence
High Level GPU Architecture
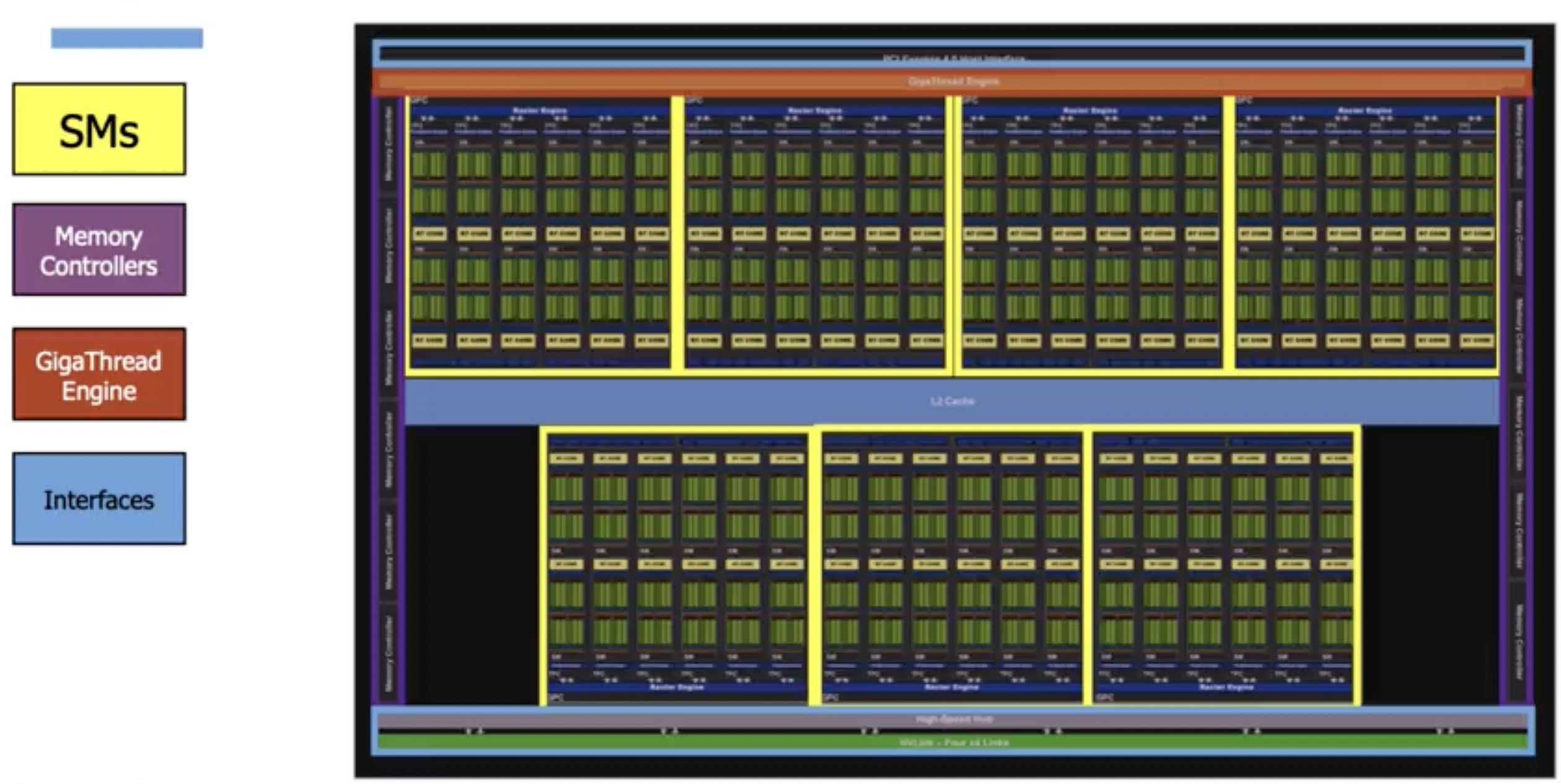
In the middle, yellow boxes are streaming multiprocessors (heart of computation). Left & right side - memory controllers which help shift and store data in diff types of memory. Gigathread engine on top is the main scheduler for different threads. Top - general IO bus interface shared between CPU & GPU to shift data Bottom - NVLink & High speed fast data transmitter interface
Streaming Multiprocessor
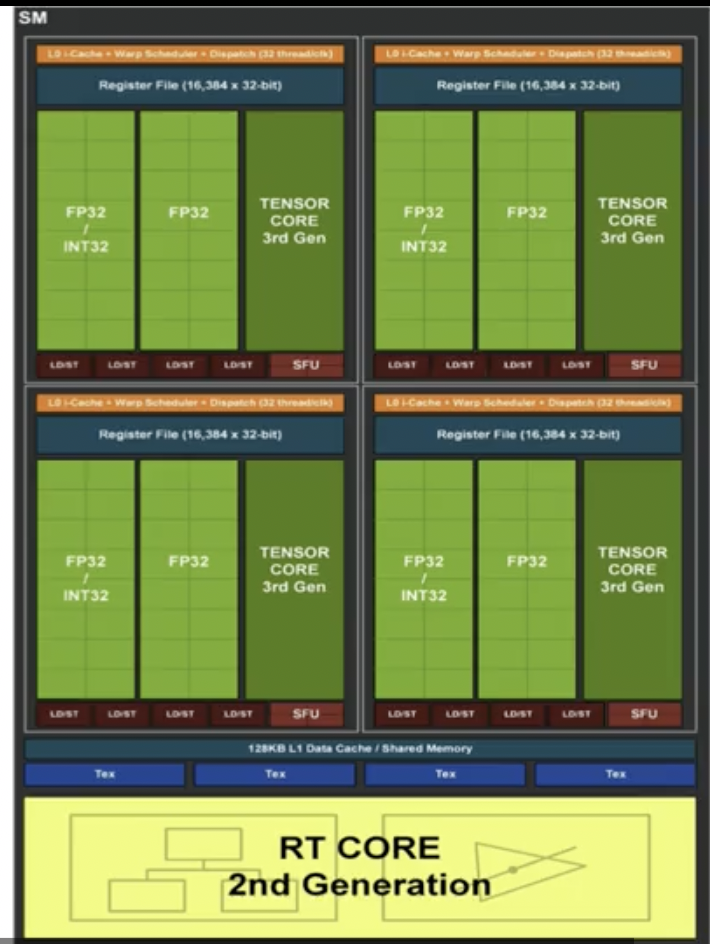
Four warps. Each warp has a L0 cache, a scheduler, collection of registers & 2 half warps. Load & store capabilities. Tensor core for each warp. L1 cache to share memory. 4 texture cores & 1 single raytracing core (dedicated to graphics processing).
Mapping between hardware & software:
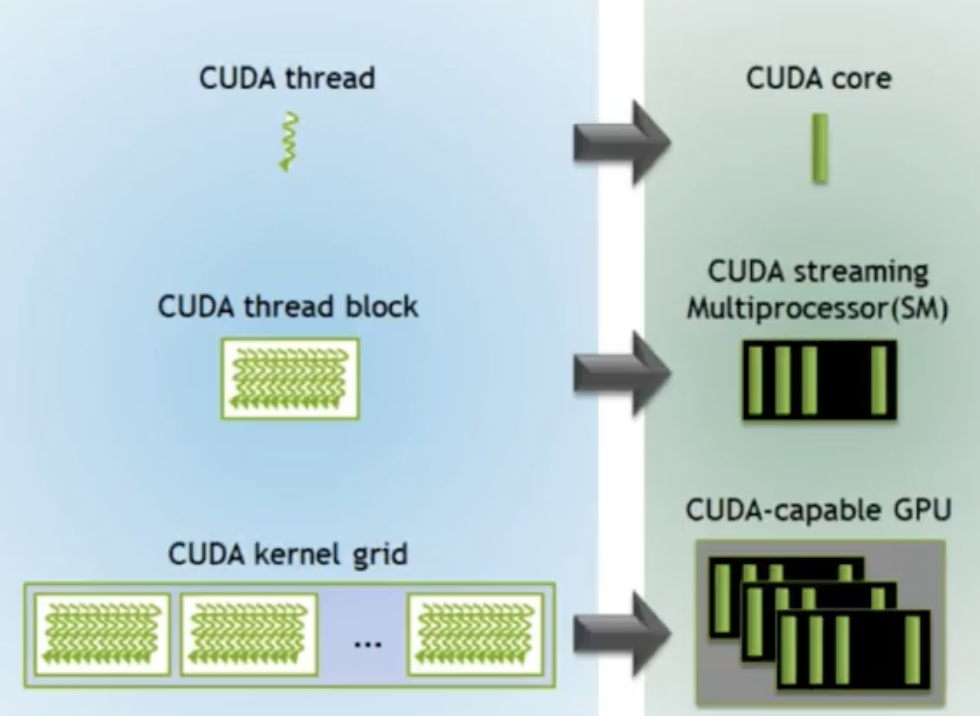
CUDA Kernel Execution:
Func<<<Dg, Db, Ns, S>>>(parameter);
^ this describes how to break up the work done on the GPU.
kernel<<<blocks, threads per block, shared_memory, stream_of_interactive_data>>>(args);
e.g kernel:
__ global __ void MatAdd(float MatA[][][], float MatB[][][], float MatC[][][])
{
int i = blockIdx.x * blockDim.x + threadIdx.x;
int y = blockIdx.y * blockDim.y + threadIdx.y;
...
}
Merge Sort algorithm: CPU -> GPU


CUDA Kernel Threads & Block syntax
1-dimensional layout: Kernel«<blocks, threads_per_block»>(parameters);
/# define N 1618
...
add<<<1, 32>>>(a,b,c);
device code(kernel):
\_\_global\_\_ add(int *a, int *b, int *c){
int idx = blockIdx.x * blockDim.x + threadIdx.x
if (idx < N) {
c\[idx] = a\[idx] + b\[idx]
}
}
2-dim layout: kernel«<grid, block»>(parameters);
/# define N 512
dim3 grid(1,1);
dim3 block(32,32);
matrixMultiply<<<grid, block>>>(matrix_a, matrix_b, output_matrix);
device code(kernel):
\_\_global\_\_ matrixMultiply(int * matrix_a, int * matrix_b, int * output_matrix) {
int x = blockIdx.x * blockDim.x + threadIdx.x;
int y = blockIdx.y * blockDim.y + threadIdx.y;
int index = x + y*N;
if (x < N && y < N) {
c\[index] = a\[index] * b\[index]
}
}
3-dimensional layout: kernel«<grid, block»>(parameters);
/# define N 16
dim3 grid(1, 1, 1);
dim3 block(N, N, N);
matrixSubtract<<<grid, block>>>(matrix_a, matrix_b, output_matrix);
device code(kernel)
\_\_global\_\_ matrixSubtract(int * matrix_a, int * matrix_b, int * output_matrix) {
int index = blockIdx.x * blockDim.x * blockDim.y * blockDim.z
+ threadIdx.z * blockDim.y * blockDim.x
+ threadIdx.y * blockDim.x + threadIdx.x;
if (index < N*N*N) {
c\[index] = a\[index] - b\[index]
}
}
We could also go 2 - 6 dimensional similar to the above. Explainer Link
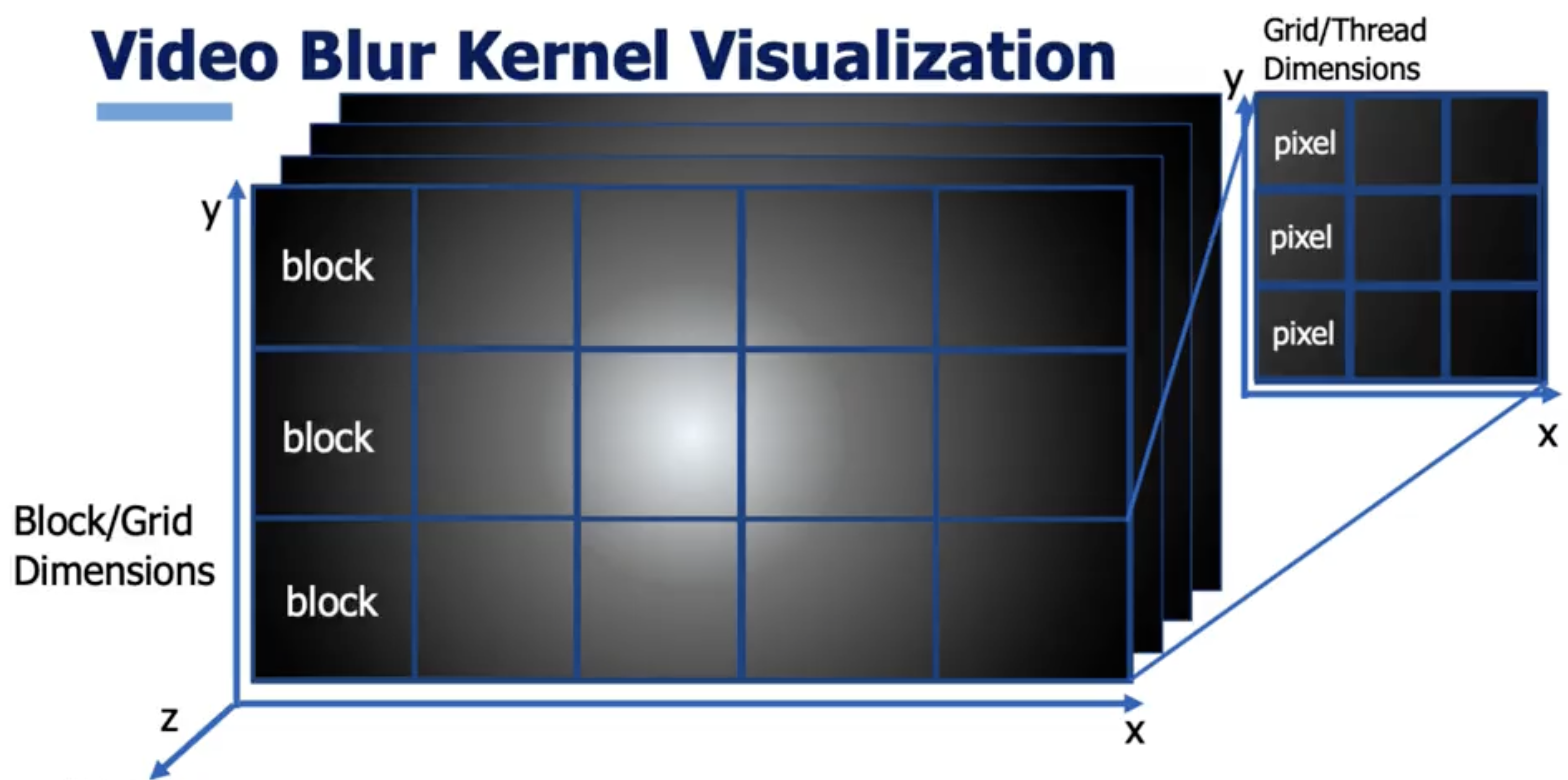
CUDA Gaussian Blur 3D Kernel