[Course 1 of the deeplearning.ai specialization on coursera]
Basics of Neural Networks -
If we use logistic regression for binary classification of images e.g. cat vs non-cat.
So an image is a 64x64x3 matrix of rgb values - unroll them into a single row of 12288 (n) length vector (features).
If we have m training examples, create a matrix of m columns and n rows.
Labels for the training examples = a (1, M) matrix.
Logistic Regression:
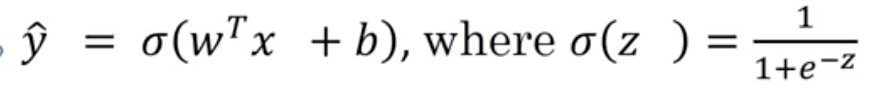
y_pred = sigmoid(WtX + b) where sigmoid(z) = 1/(1 + e^-z)
Loss function - Can’t use squared error, need alternative:
Loss(y^, y) = -y*log(y^) + (1-y)*log(1-y^)
If y = 1, want y^ large
If y = 0, want y^ small

Loss function is the error for a single training example, while the cost function computes the average of losses for the entire training set.
We can view logistic regression as a very small neural network.
Computation Graph:
If we try to compute a function J(a, b, c) = 3(a + b*c)
First compute u = b*c, then compute v = a+u, then finally J = 3*v.
Put these 3 steps in a computation graph. This is useful when there is some special output that we try to minimize. In case of lr, we try to minimize the cost function, left to right, from a/b/c to u/v and J (forward computation). To compute derivates, we compute the opposite direction (backprop).
Computing derivates:
As J = 3v, dJ/dv = 3.
And as v = a+u, dJ/da = 3 (Chain rule: dJ/da = dJ/dv * dv/da)
Final output variable: J => d(FinalOutputVariable)/dvar
(In python, generally call this dJ/dvar or just dvar)
Most efficient way to compute derivates is to follow right-to-left direction.
e.g. dJ/db = dJ/dv * dv/du * du/db = 3 * 1 * 3 = 9
Gradient descent for logistic regression:
z = transpose(W) * x + b
y^ = a = sigmoid(z)
Loss fn = -y*log(a) - (1-y)*log(1-a)
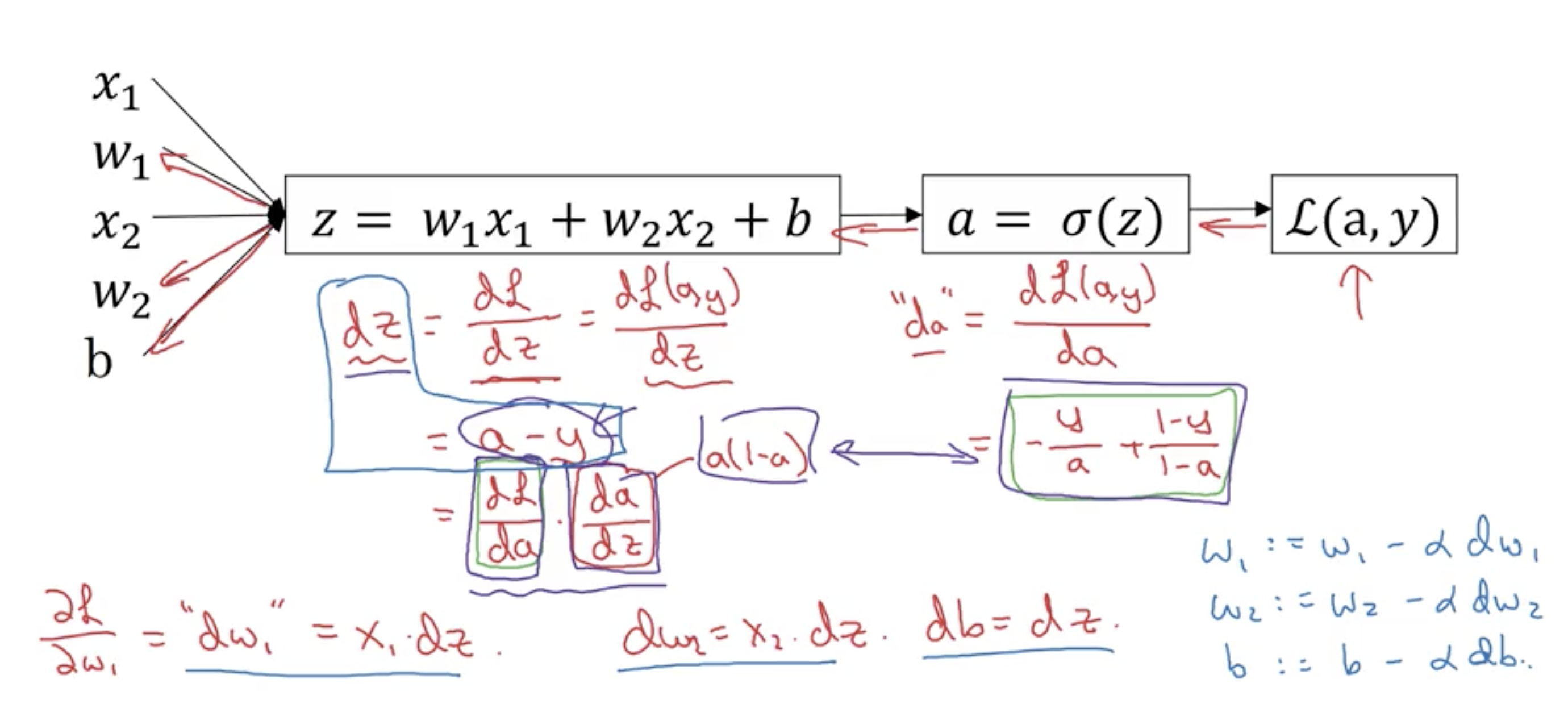
Compute gradients in the opposite direction of the computation graph. Finally perform gradient descent with alpha using computed derivates of dw1, dw2, db.
Gradient descent on m examples:
Overall dw1 for all m examples = average dw1 for each example = (1/m) * sum(dw1 for each example)
J = 0, dw1 = 0, dw2 =0 , db = 0
for i = 1 to m:
zi = transpose(w)*xi + b
ai = sigmoid(zi)
J = - [yi * log ai + (1-yi) * log (1-ai)]
dzi = ai - yi
dw1 += x1i * dzi
dw2 += x2i * dzi
db += dzi
J /= m
# dw1 and dw2 and db are accumulators, finally average them
dw1 /= m
dw2 /= m
db /= m
# now increment gradient
w1 = w1 - alpha * dw1
w2 = w2 - alpha * dww
b = b - alpha * db
Use vectorization techniques to get rid of explicit for loops (which are not efficient in deep learning)
Vectorization:
In non-vectorized implementations, we use for loops over the feature vector. e.g.
a = np.random.rand(1000000)
b = np.random.rand(1000000)
c = np.dot(a, b) # ~2ms
c = 0
for i in range(1000000):
c += a[i]*b[i]
# ~ 475ms or 200 times slower
Built-in functions use SIMD - single instruction multiple data - GPU parallelism for faster computations. (Whenever possible, avoid explicit for loops).
e.g. np.exp(v) to apply element-wise exponential, np.log(v), np.maximum(v, 0), 1/v etc
Vectorizing Logistic Regression (no for loops!)
To find forward propagation calculations:
Previously, zi = wT*xi + b and ai = sigmoid(zi)
Now, using np.dot to multiply 1xN w matrix with NxM x matrix, we get 1xM Z matrix result:
Z = np.dot(transpose(w), X) + b
Now, A = sigmoid_for_matrix(Z)
To find backward propagation derivatives:
Previously, dzi = ai - yi
Now, dZ = A - Y # Y = [y1, y2 … ym]
Previously, dw1 += x1i * dzi
Now, dW = 1/m * X * tranpose(dZ)
And dB = np.sum(dZ) / m
Finally, a highly vectorized implementation:
Z = np.dot(transpose(w), X) + b
A = sigmoid(Z)
dZ = A - Y
dW = 1/m * X * transpose(dZ)
dB = 1/m * np.sum(dZ)
W = W - alpha * dW
B = B - alpha * dB
Neural Network Basics
Each layer of neural network computes z,a entirely once.
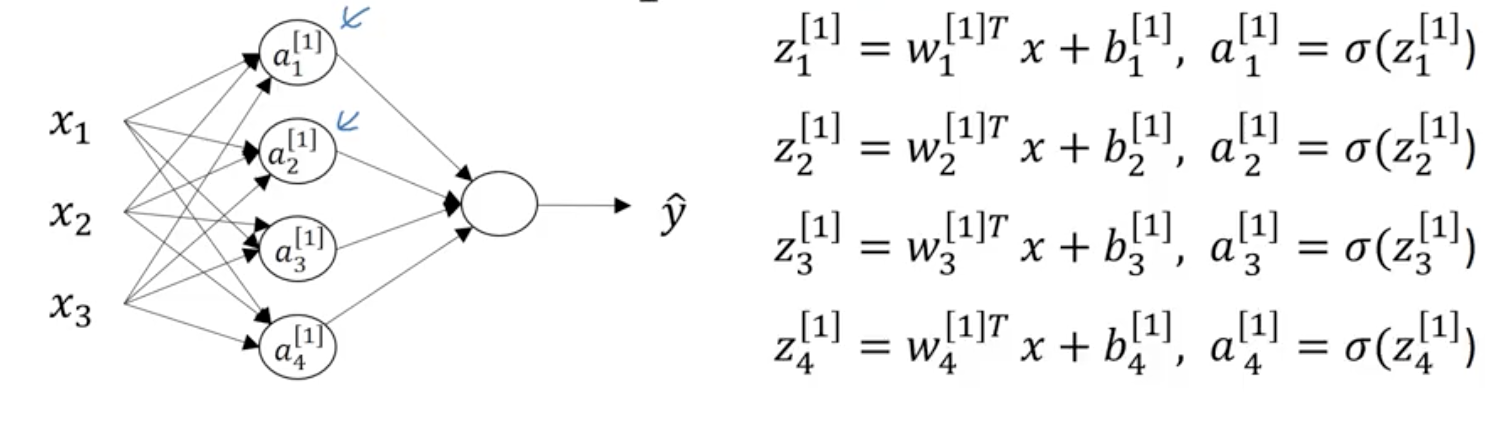
Input features - input layer of neural network
Hidden layer - inner layer
Final layer - just 1 node or output layer (generates predicted value y). Input layer not counted.
Hidden layer will have parameters w and b
w = 4x3 matrix (because 4 nodes and 3 inputs for each node)
b = 4x1 because 4 nodes
Computing a neural network output:
Z = transpose(W) * X + B (Vectorized implementation of computing output of hidden and output layers)

Vertical rows = nodes in a single layer, horizontal columns = m training examples
Pseudo code for forward propagation for the 2 layers:
for i = 1 to m
z[1, i] = W1*x[i] + b1 # shape of z[1, i] is (noOfHiddenNeurons,1)
a[1, i] = sigmoid(z[1, i]) # shape of a[1, i] is (noOfHiddenNeurons,1)
z[2, i] = W2*a[1, i] + b2 # shape of z[2, i] is (1,1)
a[2, i] = sigmoid(z[2, i]) # shape of a[2, i] is (1,1)
Lets say we have X on shape (Nx,m). So the new pseudo code:
Z1 = W1X + b1 # shape of Z1 (noOfHiddenNeurons,m)
A1 = sigmoid(Z1) # shape of A1 (noOfHiddenNeurons,m)
Z2 = W2A1 + b2 # shape of Z2 is (1,m)
A2 = sigmoid(Z2) # shape of A2 is (1,m)
If you notice always m is the number of columns.
In the last example we can call X = A0. So the previous step can be rewritten as:
Z1 = W1A0 + b1 # shape of Z1 (noOfHiddenNeurons,m)
A1 = sigmoid(Z1) # shape of A1 (noOfHiddenNeurons,m)
Z2 = W2A1 + b2 # shape of Z2 is (1,m)
A2 = sigmoid(Z2) # shape of A2 is (1,m)
Activation Functions:
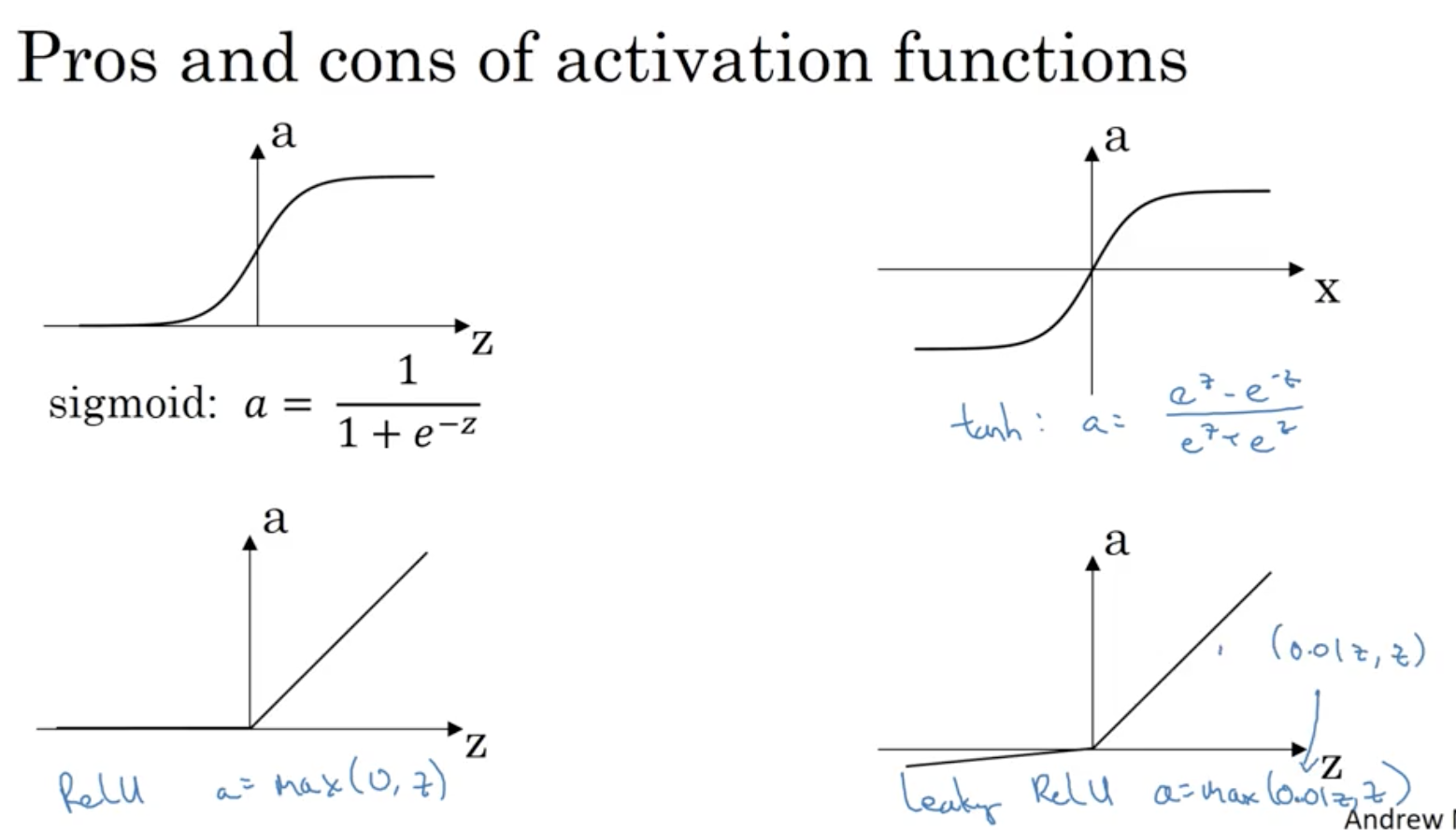
Till now, we use sigmoid function.
a = 1 / (1 + e^-z)
General case, take g(z) - can be e.g. = tanh(z)
= (e^z - e^-z) / (e^z + e^-z)
For hidden units, if g(z) = tanh, generally works better than sigmoid function.
Because mean of activations = 0 in tanh, so better for data to have mean closer to 0, makes learning for next layer easier. (except in output layer)
Another choice is ReLu (rectified linear unit) = max(0, z) - default choice for linear layer.
Neural network will learn faster using ReLu because slope of ReLu is not 0 (like tanh or sigmoid)
Why do we need non-linear activation functions: If a = z, then neural network will output linear function of the input (No matter how many layers). We need a non-linear activation function in between somewhere, otherwise composition of linear functions will always output linear functions.
Derivatives of activation functions
Derivation of Sigmoid activation function:
g(z) = 1 / (1 + np.exp(-z))
g'(z) = (1 / (1 + np.exp(-z))) * (1 - (1 / (1 + np.exp(-z))))
g'(z) = g(z) * (1 - g(z))
Derivation of Tanh activation function:
g(z) = (e^z - e^-z) / (e^z + e^-z)
g'(z) = 1 - np.tanh(z)^2 = 1 - g(z)^2
Derivation of RELU activation function:
g(z) = np.maximum(0,z)
g'(z) = { 0 if z < 0
1 if z >= 0 }
Derivation of leaky RELU activation function:
g(z) = np.maximum(0.01 * z, z)
g'(z) = { 0.01 if z < 0
1 if z >= 0 }
Gradient Descent for Neural Networks
Formulas for computing derivates - TODO
Random Initializations: If we initialize weights to 0 - then all nodes in a layer will compute the same result. And during backpropagation, dZ will also be same for all nodes (because symmetric output). So both hidden units will compute the same function for however many iterations. This is not helpful because diff hidden units should compute different functions.
Initialize to very small random values. Then units will not have symmetry breaking problem. If random weights are too large, then activation values are more like to end up at flat slopes of tanh/sigmoid - gradient descent would be very slow.
For deep neural networks, can pick diff constant than 0.01.
Intuition for back propagation:
Neural network gradients - da2, dz2, da1, dz1
The computation for multiple steps are usually collapsed into 2 steps.
Deep L-Layer Neural Network
- Logistic regression - shallow model
- 1 hidden layer - 2 layer network, still shallow
- 2 hidden layers
- 5 hidden layers
Notation -
4 layer NN, 5 units in 1st layer, 5 in 2nd, 3 in third, 1 output unit
So L = 4 # number of layers
n[2] = # units in layer 2
So n[1] = 5, n[2] = 5, n[3] = 3, n[4] = 1 and input layer n[0] = 3
a[i] = number of activations in layer L. In forward prop:
a[L] = g[L] (z[L])
w[L] = weights for z[L]
b[L] = bias for z[L]
a[0] = x # x are the inputs and also the activations for layer 0
a[L] = yhat # final activation
Forward Propagation in a Deep Network
For a single training example:
For layer 1, z[1] = w[1] * x + b[1] # x = a[0]
a[1] = g[1] (z[1])
For layer 2, z[2] = w[2] * a[1] + b[2] # input for layer 2 is output a[1] from layer 1
a[2] = g[2] (z[2])
… etc
Finally, z[4] = w[4] * a[3] + b[4]
a[4] = g[4] (z[4]) == yhat
Generally, z[L] = w[L] * a[L-1] + b[L-1]
a[L] = g[L] (z[L])
For m training examples in a vectorized way:
Z[1] = W[1] * A[0] + B[1] # A[0] = X
A[1] = G[1] (Z[1])
Z[2] = W[2] * A[1] + B[2]
A[2] = G[2] (Z[2])
So 2 matrices, for Z and A. m columns are training examples. L rows are layers => for L = [1..4]
Ok to have explicit for loop for all layers from 1 to L.
Getting matrix dimensions right
Use a piece of paper to work through the matrix dimensions:
L = 5
n[0] = 2, n[1] = 3, n[2] = 5, n[3] = 4, n[4] = 2, n[5] = 1
z[1] = 3 x 1 # 3 z activations for each hidden unit in the first layer
x[1] = 2 x 1
So w[1] should be something that when multiplied by input (n[0] x 1) matrix, should give z[1] = 3x1 matrix
e.g. w[1] * (2 by 1) == (3 by 1)
Thus w[1] = (3, 2)
Generally, w[1] = (n[1] by n[0]) dim matrix
More generally, w[L] = (n[L], n[L-1])
e.g.
Dimension of w[2] = 5 by 3
Dimension of w[3] = 4 by 5
Dimension of w[4] = 2 by 4
Dimension of w[5] = 1 by 2
For bias b vector, the dimension should be same as z dimension i.e. (n[L] by 1) vector
Generally, dimension of b[L] = (b[L], 1)
For back propagation, dimensions of dw = dimension of w = same (n[L] by n[L-1])
db = same dimension as b = n[L] by 1
z = g(a) hence z and a should have the same dimensions.
For vectorized implementations:
Dimensions of z, a and x will change, but w, b, dw, db stay the same.
Dimension of z= m training examples so (n[L] by m)
Dimension of w = same (n[L] by n[L-1])
Dimension of X/A = (n[L] by m) (instead of n[L] by 1)
Dimension of b = same (n[L] by 1), which gets broadcasted to (n[L] by m) automatically
dZ and dA = same dimension as Z, A = (n[L] by m)
Simple to complex hierarchical representation - compositional representation - e.g. finding edges first, then faces.
So deep neural network with multiple hidden layers might be able to have the earlier layers learn these lower level simple features and then have the later deeper layers then put together the simpler things it’s detected in order to detect more complex things like recognize specific words or even phrases or sentences.
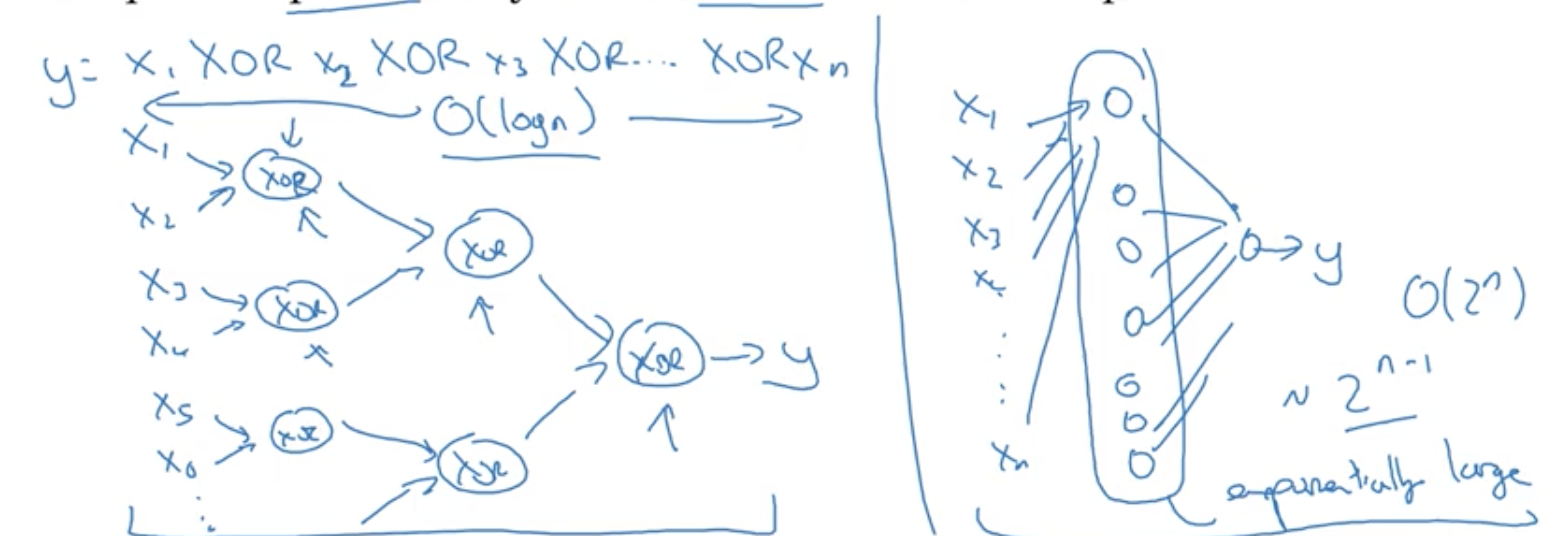
Circuit theory - there are functions which can be computed with a “small” L-layer deep neural network that shallower networks would require exponentially more hidden units to compute
e.g. XOR has a log speedup with multiple layers, while a single layer needs to compute 2^n possible configurations.
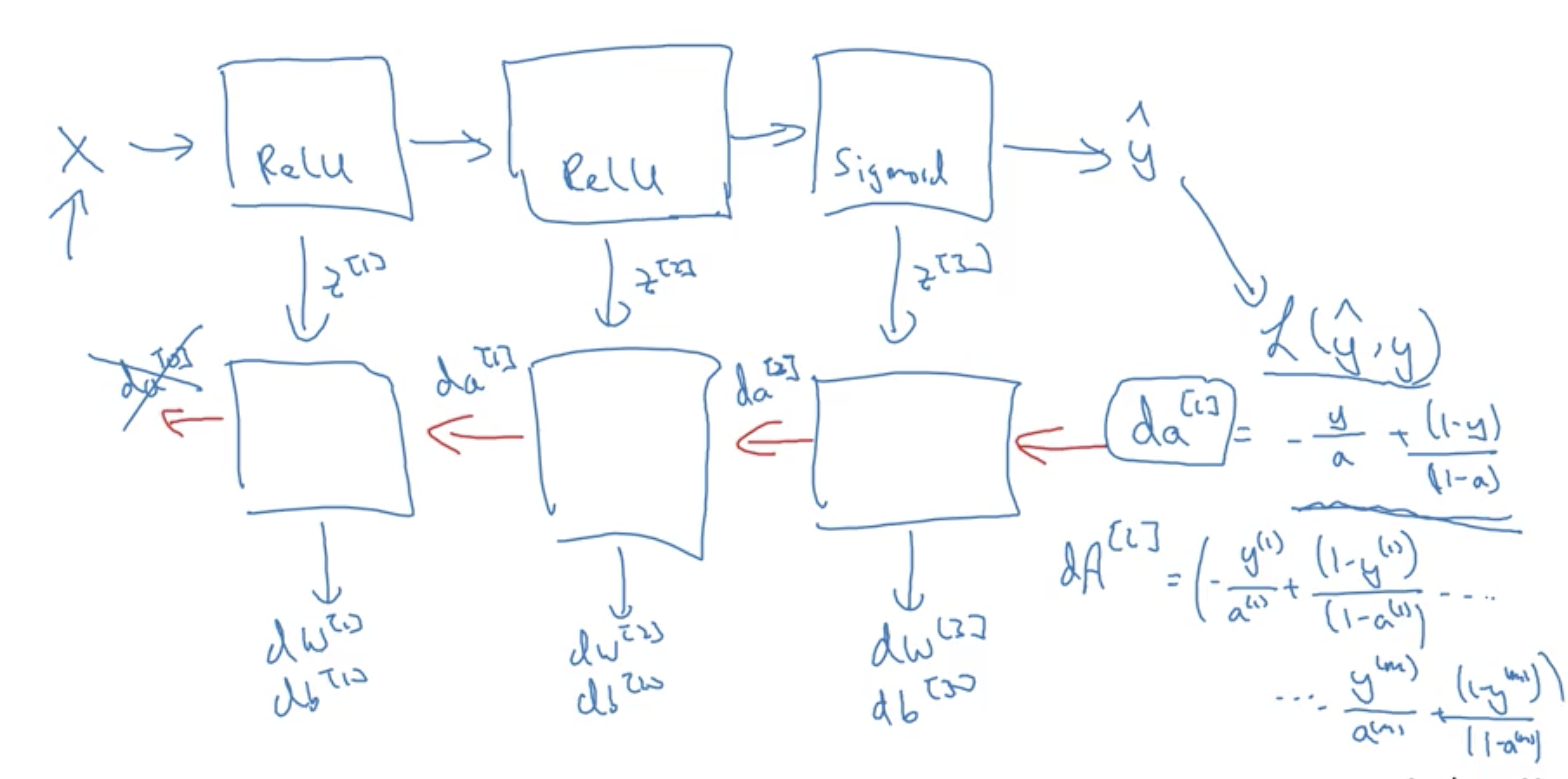
Implementation of forward/backward propagation
Forward prop step, backward prop step, and cache to store values of Z for each cell.
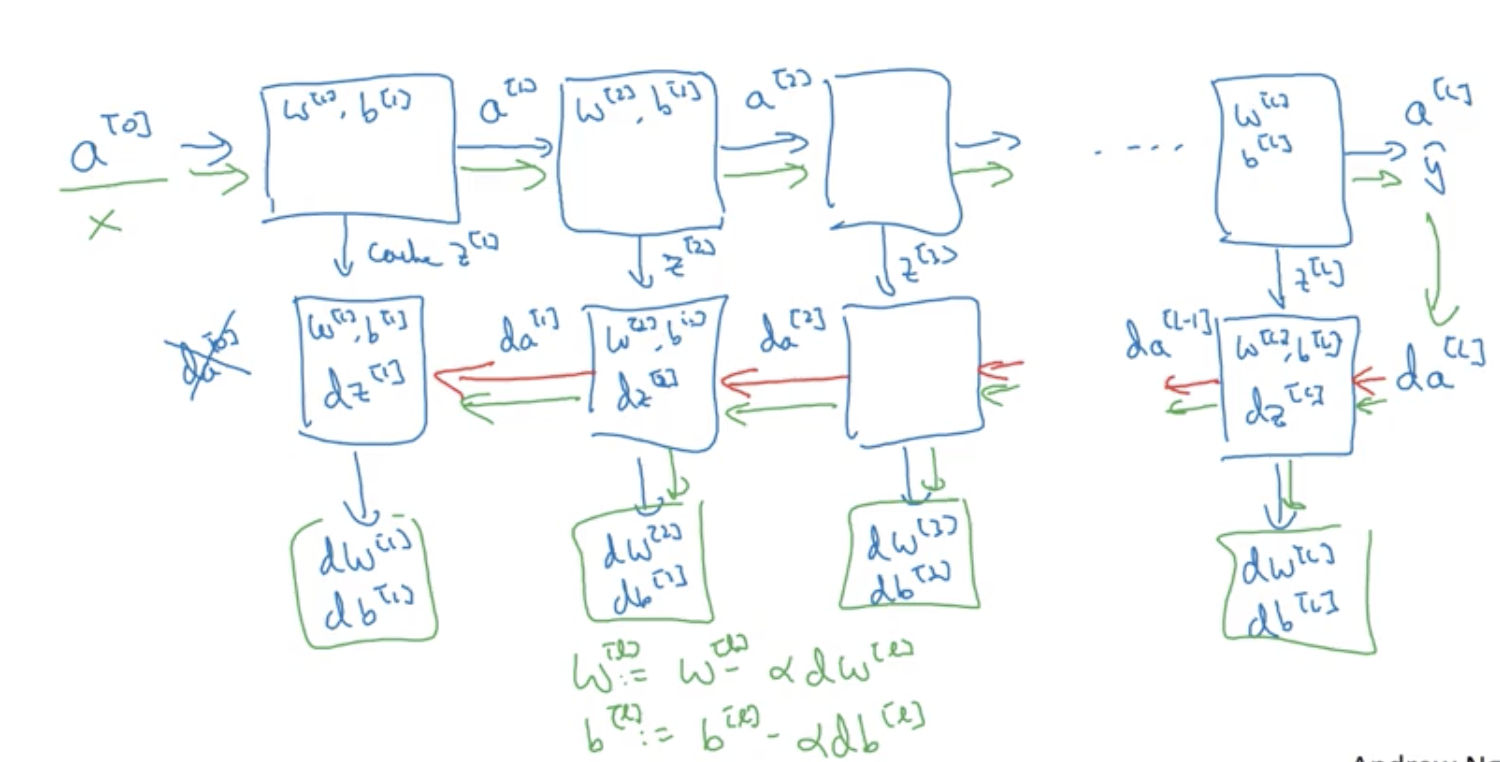
Z[L] = W[L] * A[L-1] + B[L]
A[L] = g[L] ( Z[L] )

Parameters vs Hyperparameters
Parameters: w[1], b[1], w[2], b[2] …
Hyperparameters:
- learning rate alpha
- number of iterations/epochs
- number of hidden layers L
- number of units in each layer n[1], n[2]
- activation fn used
Later on: momentum, mini batch size, regularization params etc
Empirical process to test idea in code, then adjust hyper parameters etc. We can see the learning rate by plotting the graph of cost J vs # of iterations etc
